Particle jumps in shallow standing wave traps

We focused here on the behaviour of a sphere trapped in a single focused Gaussian beam while the beam focus approached the dielectric interface with small (water-glass) or medium (water-dielectric layers) reflectivities. We observed sudden jumps of the sphere from its previous equilibrium position to a new and more stable one. We measured this behaviour and succesfully compared with our theoretical model.

The incident beam comes through the coverslip towards the microscope slide where it is retro-reflected upwards. Both counter-propagating beams interfere, create a standing wave but its visibility is highest near the microscope slide (see the figure).  If the reflectivity of the surface is rather low, there exists one deep optical trap with an envelope modulated by the standing wave. Therefore, under proper circumstances there could exist several possible equilibrium positions.When the waist of the incident beam approaches the surface, the potential profile changes and some of the standing wave traps becomes depper than the previous one and so the shere jumps. We proved that the magnitude of these jumps between the neighbouring equilibrium positions can be decreased by a suitable size of the sphere.

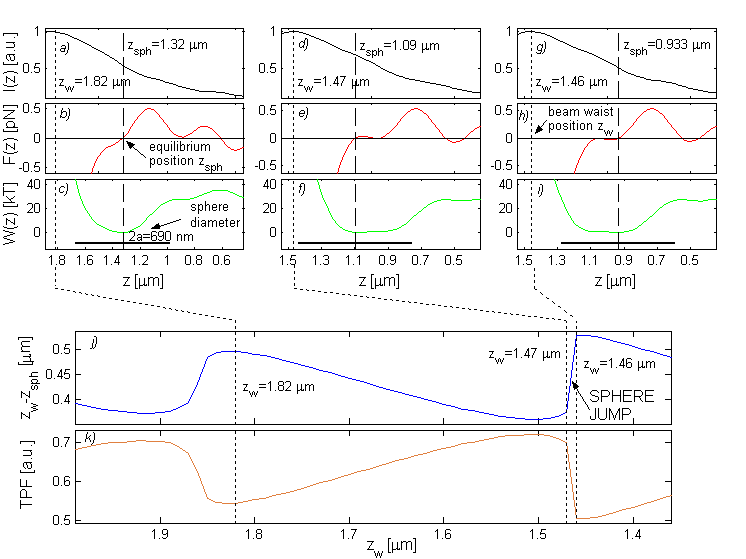
Calculations explaining the origin of the sphere jumps when the trapping beam waist approaches the surface. The plots a – i show the theoretical profiles of the on-axis intensity I(z)=[E_x(z)]²+[E_y(z)]²+[E_z(z)]² (where E_x(z), E_y(z), E_z(z) are on-axis components of electric field vector) in the first row, axial force F(z) in the second row, and depth of the potential well W(z) in the third row as the functions of the sphere-surface distance z at three chosen positions of the beam waist z_w. The trapped sphere is located at z_sph (places of zero force and potential minima). The modulations of the envelopes of the single beam intensity, force, and potential are caused by the interference of the incident and reflected waves. This causes that more than one probe equilibrium position exist and they could fuse together and create a wider potential well while the beam waist approaches the surface (see plots d – f). Only 10 nm shift in the beam waist position then causes deformation of the potential well bottom in such a way that the sphere equilibrium position moves by 157 nm (see plots d – i). This change results in a sphere jump of 157 nm further away from the beam waist position (closer to the surface). The distance between the beam waist and sphere equilibrium positions (z_w–z_sph) is shown in plot j as the function of the beam waist position. Plot k shows how the two-photon fluorescence ixcited by the beam in dyed sphere (proportional to the square of the optical intensity) depends on the position of the beam waist. Since the trapping beam intensity is different at each equilibrium position, the two-photon fluorescence is another sensitive indicator of the non-uniform sphere motion due to the influence of the reflected wave (see plot k). The simulation results were obtained for polystyrene sphere of radius equal to a=345 nm (see the thick lines in plots c, f, i), water-glass interface of reflectivity R=0.4%, laser power P=10 mW, beam waist size w₀=0.4 mm, sphere and water refractive index n_sph=1.585 and n_wat=1.332, respectively.

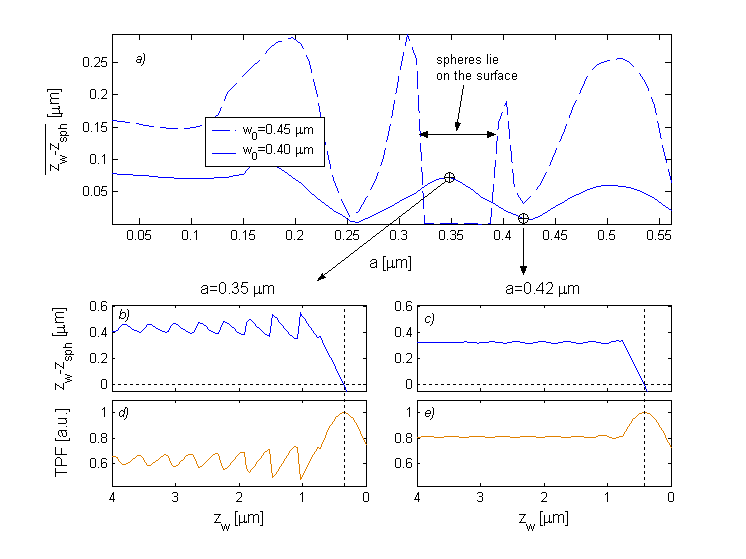
It was already shown (here) that the maximal axial force in the standing wave trap depends on the sphere size and for certain sphere radii the influence of the standing wave is supressed. We deduced that similar effect must exist also at lower surface reflectivities and its existence should decrease the length of the sphere jump between equilibrium positions. Therefore, we proceeded to more extensive simulations and analysed how the length of the sphere jumps depends on the polystyrene particle radius and beam waist size. As shown in the following figure, the length of the jumps can be indeed reduced by appropriate size of the sphere. This standing-wave-eliminating sphere radius also depends on the beam waist size (it slightly decreases with increasing beam waist).

Description of the figure: Dependence of the jump length on the polystyrene sphere size. Using the procedure described in the previous figure we analysed behaviour of trapped polystyrene spheres (radii from 30 nm to 570 nm) during the beam waist approaching the surface from the distance of 4 mm. The results of this analysis are shown in plot a for two beam waist sizes (w₀=0.40 mm and w₀=0.45 mm). The quantity z_w–z_sph is an average value of 5 subsequent jump lengths starting from the first jump which occurs for z_w < 4 mm. This procedure provides a smooth curve with visible tendencies of the studied effect. It is seen that a wider beam waist causes longer jumps of the sphere but it is not possible to confine spheres of radii 0.32 mm < a < 0.38 mm. We choose two representative sphere radii – one is very sensitive (a=0.35 mm) and the other is insensitive (a=0.42 mm) to the standing wave component – to show the distance of the sphere from the beam waist (z_w-z_sph) and two-photon fluorescence signal (TPF) as the function of the beam waist distance from the surface in plots b – e. In these figures, the difference in the sphere behaviour is clearly seen together with the fact that the overall maximum of TPF occurs very close to the place where the beam waist position z_w overlaps the sphere centre position z_sph (z_w-z_sph=0). We used the following parameters for the simulation: water-glass interface of reflectivity R=0.4%, laser power P=1 W, sphere and water refractive index n_sph=1.585 and n_wat=1.332, respectively.

Experimental results

To prove experimentally our theoretical conclusions we analysed the behaviour of optically-trapped fluorescently dyed polystyrene spheres while they approached the surface. We enhanced the standard experimental apparatus of optical tweezers with two independent particle position detection systems (see figure) – photomultiplier tube (PMT) to detect weak two-photon-fluorescence (TPF) which is excited in a trapped fluorescent-dyed sphere by the trapping beam and a quadrant photo-diode (QPD) which was placed behind the condenser to monitor the lateral and longitudinal motions of the sphere from the changes of the intensity pattern. The TPF signal is proportional to the square of the excitation intensity and therefore it is very sensitive to the motion of the sphere with respect to the beam waist position. However it cannot distinguish between lateral and longitudinal displacements. Therefore we used also the quadrant photo-diode (QPD). The details of the experimental procedure can be found in the publications mentioned below. 

We calculated the theoretical profiles of TPF and QPD signals for the sphere radii a=0.345, 0.41 mm and water refractive indices n_sphere=1.585 and n_water=1.332, and laser power incident on the trapped bead P=50 mW. Reflectivities of the uncoated and coated glass-water interfaces were assumed to be R=0.4% and R=13%, respectively. The only free parameter - the beam waist size w₀ - could be in principle obtained from a fit of the expected axial TPF profile shape to the experimental profile of TPF signal for the sphere lying on the surface. Because this peak is not always significant (especially for a bigger sphere) and the length of the sphere jumps depends on beam waist size (see figure), we calculated instead the theoretical profiles for w₀=0.38, 0.40, 0.42 mm and choose that value w₀ which gave a better coincidence with the measurement.

The results of both simulations and experiments are summarized in the following figures for reflectivities R=0.4% and R=13%, respectively.

Description of the figures: At the beginning of the scans (distance close to 10 mm above the reflective surfaces), the sphere is pressed against the coverslip by moving the trapping beam waist into the coverslip bulk. Afterwards, the beam waist is moved towards the reflective slide. As the beam waist approaches the sphere, the TPF signal increases till the moment the sphere is trapped and starts following the beam waist motion The decrease of the TPF signal that occurs afterwards is mainly due to the spherical aberration (caused by the refractive index mismatch between the coverslip and water), which makes the beam waist wider and consequently it decreases the on-axis intensity. We also tested the influence of the bleaching of the dye by comparing subsequent records of the TPF signals taken with a known time delay in the same direction. We found, however, that its influence is much smaller than the effect of the spherical aberrations and therefore it was not taken into account. When the beam waist approaches the reflective surface, the QPD signals also decrease. This is due to the increase of the beam width after passing through the condenser lens which in turn leads to overfilling of the detector. The effects of spherical aberration and overfilling the detector were not considered in the used theoretical model and therefore theoretical TPF and QPD profiles do not decrease as the experimental ones. As the beam waist approaches the reflective surface, the intensity modulation due to the GSW component increases and has a stronger influence on the behaviour of the trapped sphere – jumps form a saw-tooth-like structure in the profiles. It is clearly seen that these jumps are really caused by the reflection from the surface, since their size generally raises with increasing surface reflectivity. If we compare the position of sphere jumps and their length, we found a very good coincidence between the theory and experiment (see details in the plots a and b of figures 1 – general slide and 2 – reflective slide). Moreover, it is seen that the lengths of these measured jumps are indeed much smaller for bigger sphere which agrees with the conclusions from the theoretical part. More sphere radii should be tested in future to obtain the similar profiles as the one shown in figure 2a.

Conclusions

Unwanted reflections can be elliminated by the proper size of the sphere. This size depends on the reflective index of the sphere and immersion medium surrounding the sphere and slightly on the beam waist size. See experimental confirmation.

Related publications

P. Jakl, M. Sery, J. Jezek, A. Jonas, M. Liska, P. Zemanek: "Behaviour of an optically trapped probe approaching a dielectric interface",
       J Mod Opt 50, 1615-1625, 2003,    ABSTRACT   DOWNLOAD

A. Jonas, P. Zemanek, E.-L. Florin: "Single-beam trapping in front of reflective surfaces",
        Opt. Lett. 26, 1466-1468, 2001,    ABSTRACT   DOWNLOAD


Conference proceedings

P. Jakl, M. Sery, M. Liska, P. Zemanek: "How the stiffness of the optical trap depends on the proximity of the dielectric interface",
       Proceedings of SPIE 5958, 2P1-2P8, 2005,   ABSTRACT

P. Jakl, M. Sery, J. Jezek, P. Zemanek: "How the size of a particle approaching dielectric interface influences its behavior",
       Proceedings of SPIE 5514, 636-642, 2004,   ABSTRACT   DOWNLOAD

M. Sery, P. Jakl, J. Jezek, A. Jonas, M. Liska, P. Zemanek: "Influence of weak reflections from dielectric interfaces on properties of optical trap",
       Proceedings of SPIE 5036, 624-629, 2002.

P. Jakl, A. Jonas, E.-L. Florin, P. Zemanek: "Comparison of the single beam and the standing wave trap stiffnesses",
        Proceedings of SPIE 4356, 347-352, 2001,    ABSTRACT

Send comments to webmaster
Last modification: 30 Mar 2007