Retro-reflected Gaussian beam

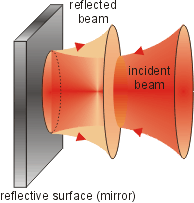
If the incident Gaussian beam is retroreflected, two counter-propagating (C-P) Gaussian beams interfere and a Gaussian standing wave is created. 

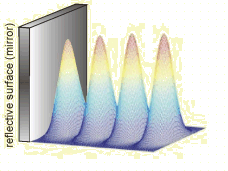Therefore the intensity maxima and minima are created along the propagatin of both beams and separation between two neighboring maxima is equal to one half of the used wavelength in the medium. Therefore, there exist steep axial intensity gradients.  If an object much smaller than the wavelength is put into the standing wave, strong gradient force localizes the object in intensity maximum. Because the Gaussian beam has intensity maximum on the optical axis, three-dimensional optical traps are created. 

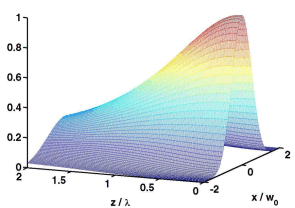
If tightly focused Gaussian beam (left image below) is retro-reflected on the mirror, due to the fast decrease of the axial beam intensity the intensity maxima of the standing wave decrease as well (see the figures).  Although several optical traps are created their properties differ significantly. 

Intensity profile of single focused Gaussian beam		Intensity profile of standing Gaussian beam

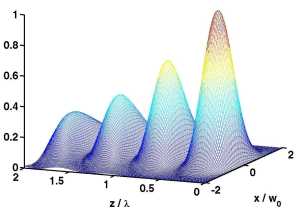Therefore the wider is the incident Gaussian beam the wider is the optical trap in radial direction and the longer is the axial array of optical traps. 

The other principle difference with respect to the single beam trap is that due to the counter-propagating beams the radiation pressure (scattering force) of both beams is partially or totally compensated. Therefore the spatially distribution of the optical intensity is the dominant effect that influences the optical trapping if both C-P beams have about the same intensity. 

Send comments to webmaster
Last modification: 30 Mar 2007