What is it a Bessel beam?
Bessel beam is one of many possible solutions of the wave equations assuming that the beam properties do not change during the beam propagation. The radial spatial profile of the electrict field is done by the Besel function. In the simplest case considered in our experiments the function is described by the Bessel function of the first kind and zero order J0. The more illustrative view is that this type of the Bessel beam is produced by an interference of plane waves with wavevectors covering the surface of a cone (see figure). This configuration can be obtain for example by an axicon illuminated by a plane wave. Due to plane wave interference behind the axicon there exists high intensity core of this so called non-diffracting beam. The bigger is the angle α0 the smaller is the diameter of the central core intensity maximum. The distance where the Bessel beam exists is done by the region where the plane waves interfere. Therefore the bigger is the diameter of the axicon and the smaller angle α0 the longer the axial distance where the Bessel beam exists.
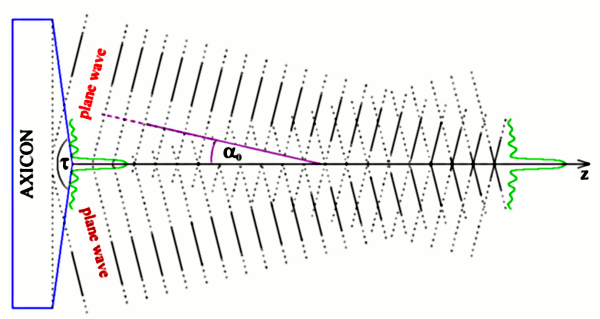
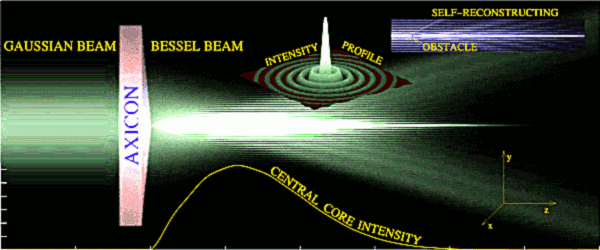
However in the real situation the axicon is not illuminated by a plane wave but by a spatially limited beam - usually Gaussian beam. Therefore the ideal properties of the Bessel beam mentioned above are not satisfied. For example the axial intensity in the beam centra is not uniform over the whole length of the Bessel beam existence even though the diameter of the beam core is the same. However the it is possible to obtain a beam having the diameter of the high intensity core in units of micrometers and existing over a milimetre range. Therefore, the axial changes of the intensity can be neglected on the micrometer range. Another important property of the Bessel beam is self-reconstruction behind the obstacle. This is extremely usefull when we consider optical trapping of more microobjects because the beam reconstructs behind the objects and preserves its properties to high degree.
Send comments to webmaster
Last modification: 30 Mar 2007

