Levitational Photonics

Our research
Over the preceding decade, levitational optomechanics has emerged as a versatile platform for addressing crucial questions in the physical sciences, ranging from the macroscopic limits of quantum mechanics to the thermodynamic limits of computation.
Our research pursues different directions:
- Non-Hermitian dynamics of single or multiple interacting optically levitating objects.
- Cooling of motion of single and multiple objects through either active feedback or passive cavity cooling.
- Developing experimental protocols for sculpting phase space of a levitated object.
- Enhancing the optomechanical interaction between the optical field and a levitated object using photonic structures. Miniaturization of experimental setups – “levitation on a chip”
- Advanced analysis of optical and random forces acting on the levitated particle.
 |
Non-Hermitian dynamics of single or multiple interacting objects. Since light is a flow of momentum, optical forces are intrinsically non-conservative. This characteristic appears whenever simple symmetries are broken. Examples include isotropic particles in circularly polarized beams [1], birefringent or non-spherical particles in linearly or circularly polarized beams [2,3], and optically interacting particles in beams with phase decoherence [4]. The forces in these systems can be locally described by a generalized Hooke’s law, having a non-symmetric stiffness matrix, resulting in biased stochastic motion]. For sufficiently high driving, or low dissipation, this bias grows until inertial forces overcome attractive forces causing a bifurcation, the formation of a limit cycle oscillation and, in multi-particle systems, synchronization [5]. [1] Svak, V. et al. Transverse spin forces and non-equilibrium particle dynamics in a circularly polarized vacuum optical trap. Nature Communications 9, 5453 (2018). |
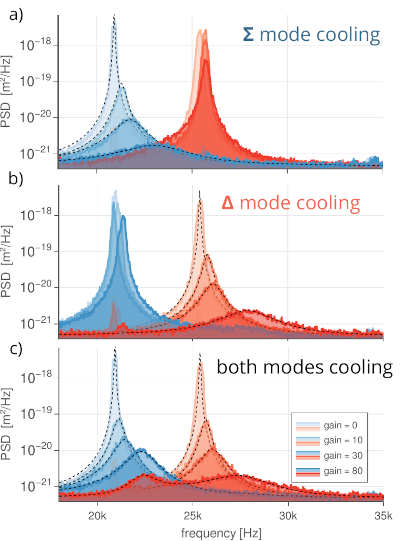 |
Cooling of motion of single and multiple objects through either active feedback or passive cavity cooling. The technique of cold damping makes use of feedback-controlled, electrostatic forces to increase dissipation without introducing additional thermal fluctuations. This process has been instrumental in the ground-state cooling of individual electrically charged nanoparticles. Here we show that the same method can be applied to a pair of nanoparticles, coupled by optical binding forces. These optical binding forces are about three orders of magnitude stronger than typical Coulombic inter-particle force and result in a coupled motion of both nanoparticles characterized by a pair of normal modes [1]. We demonstrate cold damping of these normal modes, either independently or simultaneously, to sub-Kelvin temperatures at pressures of 5 10-3 mbar [2]. Experimental observations are captured by a theoretical model, which we use to survey the parameter space more widely and to quantify the limits imposed by measurement noise and time delays. [1] Svak V. et al. Stochastic dynamics of optically bound matter levitated in vacuum. Optica 8 (2), 220-229 (2021) |
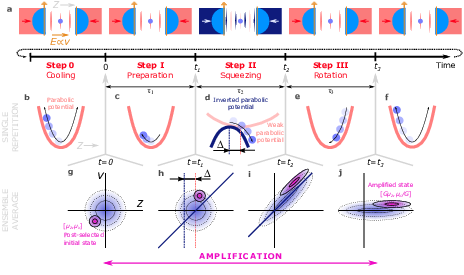 |
Developing experimental protocols for sculpting phase space of a levitated object. Using the levitated particles close to the quantum ground state for detection of ultra-weak forces or just for the proof of non-classical quantum behavior requires manipulation of the phase space probability density function (PDF or Wigner function). These PDF changes consist of extension, squeezing, amplification, or non-linear deformations. We demonstrated the function of a linear phase sensitive amplifier [1] and we analyzed its gain, linearity, extension squeezing and coherence. [1] Duchaň, M., Šiler, M., Jákl, P. et al. Nanomechanical state amplifier based on optical inverted pendulum. Commun Phys 8, 276 (2025). https://doi.org/10.1038/s42005-025-02193-z |
|
Enhancing the optomechanical interaction between the optical field and a levitated object using photonic structures. |
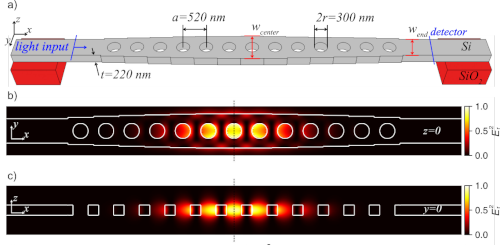 |
|
Advanced analysis of optical and random forces acting on the levitated particle Precise knowledge of an optical force profile is needed for design of sensing or quantum protocols. Quite often, only a limited amount of data is available, or the particle is in a non-stationary state far from thermal equilibrium. We develop novel methods for characterization of such optical fields based on theory of non-Markovian random processes [1] or ensemble averaging of transient trajectories [2]. |
 |

Historical roots of our research (trapping in liquid)
Before levitation in vacuum there were interesting time of trapping in liquid where we studied various aspects of optical forces in microworld.
- Dynamics of microscopic particles in various optical light fields (namely tractor beam or rocking ratchet)
- Optically assembled soft matter
- Modelling of optical tweezers
 |
Dynamics of microscopic particles in various optical light fields We employ the state-of-the art techniques to study the dynamics of microscopic objects in carefully designed optical light fields, e.g. we have demonstrated counterintuitive transport of micro particles against photon flow in so cold Tractor beam and its utilization for passive sorting of micro objects according their size. Recently, we studied behavior of particles in highly non-linear cubic potential and transport in rocking ratchet system.
|
 |
Optically assembled soft matter We study the optically mediated interaction between assembled microscopic objects - optical binding - that gives a rise to attractive and repulsive forces and dramatically influence the way such objects assemble and self-organize. This offers routes for colloidal self-assembly, crystallization, and organization of templates for biological and colloidal sciences. We focus not only on opto-mechanical aspects of optical mater but also on its photonic properties.
|
 |
Modelling of optical tweezers We are using several theoretical approaches to model interaction of light with a particle(s) in optical traps. We use in house developed codes for the Rayleigh approximation, Generalized Lorenz-Mie scattering based on approaches of Barton as well as the T-Matrix method, Coupled Dipoles Method and commercially available Finite Elements Method (Comsol Multiphysics). We focus mainly on the interaction of a non-spherical particle or large ensemble of particles in structured or interference light fields. Furthermore, we analyse both the thermal effects connected to trapping as well as stochastic behaviour of particle ensembles.
|












